- School District of Beloit
- 8th Grade - Math
8th Grade - Math
-
The School District of Beloit selected a high-quality math curriculum aligned to WI state standards that incorporates research-based instructional strategies to support all students in their mathematical learning. The goal of the math program is to prepare our students for their future, which could be very different from the world we live in today. As a result, we make an effort to establish a solid foundation in problem solving, conceptual comprehension, procedural fluency, and applying math to real-world situations. At all grade-levels, lessons build on a student’s prior math knowledge to help prepare them for future math learning.
8th Grade Units
-
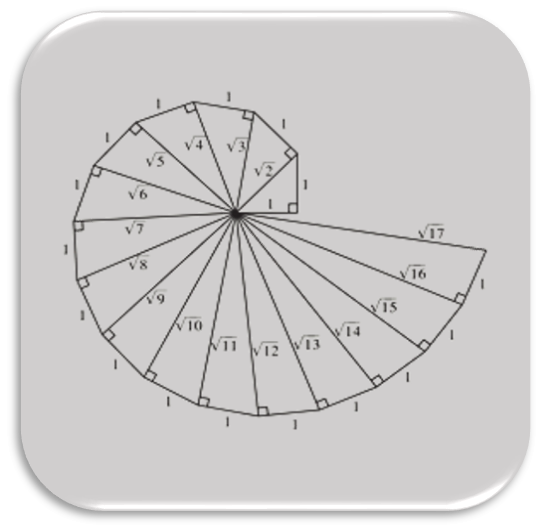
Scientific Notation, Exponents, and Irrational Numbers
Students write large positive numbers as a single digit times a power of 10 before formally defining scientific notation. Operating with large positive numbers by writing repeated factors of 10 creates a need for the properties and definitions of exponents. Students apply the properties of exponents to more efficiently find sums, differences, products, and quotients of large and small positive numbers written in scientific notation. They reason intuitively about square roots and cube roots and also explore the Pythagorean theorem, which leads to writing numbers with square root notation, approximating roots, and defining irrational numbers.
-
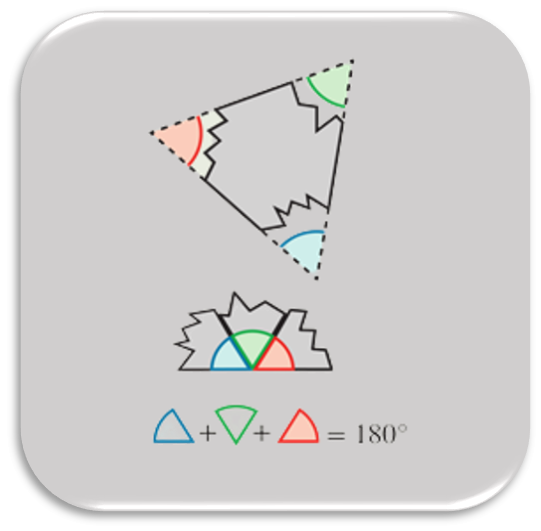
Rigid Motions and Congruent Figures
Students experience rigid motions by using a transparency to represent the movement of the plane under a translation, reflection, or rotation. They apply rigid motions to draw images of figures, and they learn to use precise language to describe rigid motions of the plane and on the coordinate plane. They define one figure as congruent to another if there is a sequence of rigid motions that maps the figure onto the other. Students apply rigid motions and the definition of congruent figures to establish facts about the angles created by parallel lines cut by a transversal. They use this new method, along with their knowledge of vertical and supplementary angles from 7th Grade, to determine the sum of the interior angle measures of a triangle and to find the relationship between an exterior angle measure and the pair of remote interior angle measures of a triangle.
-
Dilations and Similar Figures
Students analyze how dilations are different from rigid motions and scale drawings. Students draw images of figures under dilations by using a variety of tools that include transparencies, rulers, lined paper, grids, and the coordinate plane. They learn that similar figures are figures that can be mapped onto one another by using a sequence of rigid motions or dilations, or both. Students discover the angle–angle criterion for similarity and use it to determine whether two triangles are similar. They solve for unknown side lengths in similar triangles for a variety of mathematical and real-world problems.
-
Linear Equations in One and Two Variables
Students solve linear equations in one variable and discover that these equations can have only one solution, infinitely many solutions, or no solution. They then transition to solving linear equations in two variables. Students recognize that each solution to a linear equation in two variables is composed of two values which can be written as an ordered pair. Students find that there are an infinite number of solutions to a linear equation in two variables, and if they graph these solutions in a coordinate plane, the points form a line. Students use proportional relationships and similar triangles to develop an understanding of the slope of a line and then develop the slope-intercept form and the point-slope form of a linear equation.
-
Systems of Linear Equations
Students graph systems of linear equations in two variables, estimate the coordinates of the intersection point on the graph, and verify that the ordered pair is a solution to the system. They also analyze systems of linear equations to determine the number of solutions. Students find that estimating solutions from a graph is difficult for solutions composed of one or more fractional values. So they use the substitution method to write a system of linear equations in two variables as one linear equation in one variable. Now equipped with various solution methods, students are challenged to write and solve systems resulting from numerical, geometrical, historical, and real-world contexts.
-
Functions and Bivariate Statistics
Students learn that a function relates inputs and outputs in such a way that each input is assigned one and only one output. They write equations to represent linear functions, and they relate the rate of change and initial value of each function back to the context. Students use scatter plots to display bivariate numerical data. For data that appear to have a linear pattern, they draw a line that fits the data and write an equation of that line. Students examine bivariate categorical data by using two-way tables and find row or column relative frequencies to informally assess evidence of an association between two categorical variables. Students develop the volume formulas for pyramids, cylinders, cones, and spheres and use linear functions to solve real-world problems involving volume.
By the end of 8th Grade, students will...
-
- relate large and small numbers to real-world measurements and contexts.
- apply their understanding of squares and cubes to reason intuitively about square roots and cube roots.
- extend their work with powers of 10 to expressions with integer exponents.
- apply and describe sequences of rigid motions through hands-on and digital activities.
- define one figure as congruent to another if there is a sequence of rigid motions that maps the figure onto the other.
- establish facts about the angles created by parallel lines cut by a transversal by applying rigid motions and the definition of congruent figures.
- apply rigid motions to draw images of figures and learn to use precise language to describe rigid motions of the plane and on the coordinate plane.
- find images of figures under dilations by using a variety of tools that include transparencies, rulers, lined paper, a grid, and the coordinate plane.
- use the underlying idea of proportionality to solve for unknown side lengths in similar triangles for a variety of mathematical and real-world problems.
- learn how to use linear equations to write repeating decimals as fractions.
- determine that graphing the solutions in a coordinate plane forms a line.
- recognize that many equations can represent the same line.
- use proportional relationships and similar triangles to develop an understanding of the slope of a line.
- apply the skills learned to write and graph linear equations in slope-intercept form, point-slope form, and standard form.
- write and use linear equations to solve problems in real-world contexts.
- analyze systems of linear equations to determine the number of solutions.
- write and solve systems resulting from numerical, geometrical, historical, and real-world contexts.
- use scatter plots to display bivariate numerical data.
- describe any pattern of association between the variables in terms of shape, direction, and strength.
- draw a line that fits the data.
- interpret the slope and the y-intercept in context.
- observe intervals where functions increase, decrease, or neither increase nor decrease.



